
Composants Passifs et Qucs-studio
Un composant passif ne nécessite pas d'énergie pour fonctionner. Les composants passifs sont utilisés dans de nombreux circuits pour stocker ou dissiper l’énergie, filtrer les signaux et les contrôler.

Introduction
Un composant est dit passif lorsqu’il n’utilise pas de courant pour fonctionner autre que le courant alternatif du circuit auquel il est rattaché.
Lors de ce TP, nous avons étudié cinq composants passif différents, une résistance, une bobine, une quartz et deux condensateurs, un monté en surface (CMS) et un traversant (THD).
Nous avons pris la mesure du comportement de chaque composants grâce à un analyseur de réseaux ou VNA (Vector Network Analyser). Celui-ci permet de mesurer les paramètres S. Il est assez puissant pour mesurer en simultané la réflexion et la transmission générées par les composants à étudier.
Le comportement fréquentiel des composants passifs est caractérisé par le module de l'impédance en fonction de la fréquence. Le principe du VNA est donc de mesurer les paramètres S puis d’en déduire l'impédance du composant (module et phase).
Le but de ce TP est de maîtriser le fonctionnement d’un VNA ainsi que d'interpréter les mesurer faite par celui-ci.
A- Phase de calibration
Pour effectuer de bonne mesure, nous devons configurer le domaine d’analyse de l’appareil avec les paramètres suivants : (c’est mesure nous ont été donnés dans l'énoncé du TP.)
-
Fréquence de départ = 30 kHz
-
Fréquence d’arrêt = 900 MHz
-
nombre de points de mesure = 1001 points
-
facteur de moyennage = 10
-
Balayage fréquentiel = logarithmique
On configure également l’affiche de la mesure. On commence par mettre le paramètre de la mesure du coefficient de réflexion, pour cela sur le VNA nous allons dans le menu "MEAS", puis dans "Network analysis" menu et sélectionnons le paramètre "S11". Une fois cela fait, nous allons afficher le coefficient de réflexion sur l’abaque de Smith.
Dans le menu "FORMAT", puis Smith, nous sélectionnons "R+jX".
Maintenant que tout est bien paramétré, nous pouvons calibrer le VNA. Pour cela nous allons dans le menu "CAL", puis "Cal kit", ce qui va nous permettre de sélectionner le kit de calibration que l’on utilise. On sélectionne alors le kit qui nous correspond, ici pour nous, SMD 50 ohm GEII.
On calibre alors le port 1, pour cela nous retournons dans "CAL", puis "Calibrate" et enfin "1 port Cal".
Puis nous suivons le principe de calibration de base :
-
On branche en circuit ouvert → on lance la mesure (OPEN)
-
On branche en court-circuit → on lance la mesure (SHORT)
-
On branche avec une charge de 50 Ohm → on lance la mesure (LOAD)
-
On vérifie tout le temps sur l’abaque si on a bien le résultat attendu (tableau 1)
Le calibrage se fait à l’aide d’un kit qui est différent des composants que l’on va ensuite mesurer, donc pour avoir le bon calibrage au niveau des composants, nous devons ajouter un “offset”, une extension des plan de références pour cela nous allons dans le menu "CAL", puis "Port extension", "1 port Cal" et on met sur ON. On étend ensuite le plan de référence du bout du câble jusqu’à la position des futurs composants. Dans le menu "CAL", on va dans "Port extension", puis "1 port Cal" et nous rentrons la valeur de 107ps.
Résistance 50 Ohms
Court circuit
Circuit Ouvert

Résistance
Quartz
Bobine
Condensateur CMS
Condensateur THD
Figure 1 : Platine de calibrage
OPEN
SHORT
LOAD
Résultats attendus
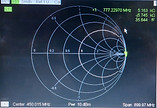
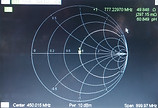
Nous devons obtenir un point tout à droite de l’abaque.
Nous devons obtenir un point tout à gauche de l’abaque.
Nous devons obtenir un point au centre de l’abaque, adaptation d’impédance.
Résultats obtenus

Z = ∞ Ω
z = ∞
Z = 0 Ω
z = 0
Z = 50 Ω
z = 1
Tableau 1 : Calibration VNA
Ici, dans les trois cas, la partie imaginaire est nulle. On le voit notamment avec les points qui sont tous les trois sur la ligne des réel pur (ligne des abscisses).
Les impédances réduites sont toutes égales à leur impédance ormi celle en charge qui est de 1 car l'impédance réduite est égale à l’impédance divisée par l’impédance du circuit. Ici elles sont égale donc impédance réduite de 1.
Nous affichons maintenant l’impédance sur le diagramme à la place du coefficient directeur. Pour cela nous allons dans le menu MEAS, puis dans impedance Analysis menu et nous sélectionnons le symbole du module de l’impédance |Z|.
On configure ensuite l'affichage pour qu'il soit en logarithme. Dans le menu SCALE, on sélectionne Y-axis et on choisit Log.
Pour relever des valeurs, nous pouvons utiliser des curseurs comme sur l'oscilloscope. Pour cela, dans le menu MARKER, on sélectionne le marker 1 puis on tourne la molette pour positionner le marqueur à l'endroit souhaité.
Si besoin, nous pouvons adapter l'affichage vertical pour nous permettre de voir en intégralité les courbes. Pour cela il suffit dans le menu SCALE de sélectionner l'autoscale. Qui est ni plus ni moins un paramètres nous permettant de mettre automatiquement les paramètres les plus adaptés à la situation.
Si on teste les paramètres sur un composant, par exemple ici le condensateur THT, on obtient la courbe suivante sur le diagramme de Smith.
.jpg)
Figure 2 : Impédance condensateur THT
B- Mesures
Nous commençons par mesurer le comportement fréquentiel de chaque composant sur le VNA et nous téléchargeons le fichier de mesure (.S1P) qui nous servira par la suite au calcul du schéma équivalent de chacun de ces derniers.

Résistance
Quartz
Bobine
Condensateur CMS
Condensateur THD
Figure 3 : Platine de test
Nous passons ensuite sur QucsStudio. Ce logiciel nous permet de faire des simulations de circuit électronique. Grâce à celui-ci, nous allons donc pouvoir déterminer les valeurs des composants parasites grâce à deux méthodes.
C- Calculs
Nous souhaitons être en capacité d’exprimer les effets parasites de chaque composant. En effet chaque composant possède un schéma équivalent qui représente ces effets là. Nous allons donc utiliser deux méthodes pour caractériser les composants de leurs schéma équivalent.
Méthode 1 (par calcul) :
Le condensateur traversant (THD)
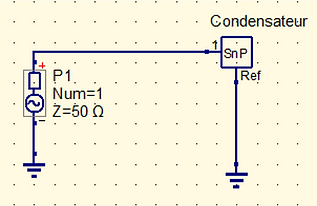
Dans cette méthode, nous allons d’abord simuler avec les valeurs relevées avec le VNA pour le condensateur traversant. Pour cela, nous avons fait un circuit avec en entrée une source avec une impédance de 50 Ohm et nous avons mis ensuite composant nous permettant de récupérer les valeurs précédemment enregistrées.
.png)
Figure 4 : Importation des fichiers S1P
.png)
Figure 5 : s-parameter
Nous lançons ensuite la simulation, pour cela, il faut mettre un composant nous permettant de le faire et le paramétrer correctement.
Ce composants est paramétré en suivant :
-
Type → Logarithme
-
Start → 300 kHz
-
Stop → 1.3 GHz
-
Points → 2001
On lance alors la simulation et on obtient les courbes suivantes :
.png)
Figure 6 : Coefficient de réflexion condensateur THD
Le diagramme de Smith correspond bien à ce que nous avions sur le VNA. Ce qui nous permet de certifier le bon fonctionnement de notre simulation.
Nous pouvons ensuite tracer le module et la phase de notre impédance sachant que seul le module va nous être utile pour la suite. Pour les tracer, nous cherchons, dans la liste de tous les composants, les diagrammes cartésiens. Dans ces paramètres, nous avons tracé la fonction mag(Z1) où Z1 est la fonction rtoz du coefficient de réflexion S[1,1] (cette fonction permet de convertir le coefficient de réflexion en impédance) et où la fonction mag( ) permet de faire le module. On trace donc le module de Z1 en fonction de la fréquence, on obtient alors le graphique suivant.
.png)
Figure 7 : Comportement de l’impédance en fonction de la fréquence
Sur un autre graphique cartésien, nous avons tracé la fonction phase(Z1) où la fonction phase( ) permet de faire la phase. On trace donc la phase de Z1 en fonction de la fréquence, on obtient alors le graphique suivant.
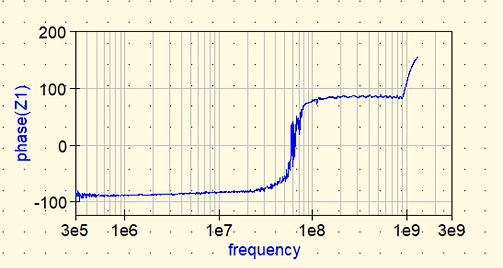.png)
Figure 8 : Phase condensateur THD
Un condensateur réel est équivalent au schéma suivant :
.png)
Figure 9 : Schéma équivalent condensateur THD
Comme dit plus tôt, nous nous concentrons sur la courbe du module. Dans un premier temps, nous avons calculé la valeur du condensateur. Pour cela, nous avons placé un curseur sur la courbe du module à l’endroit qui correspond à un condensateur et nous avons relevé la valeur de la fréquence et la valeur du module pour le calcul du condensateur.
.png)
Figure 10 : Mesure effet capacitif condensateur THD
Pour obtenir le calcule du condensateur, on par de l’expression de l’impédance équivalente :
Zeq=ZR+ZC+ZL
⇔ Zeq=R+1/jCω+jLω
En basse fréquence on a : |Zeq|=1/|Cω|
On obtient donc C=1/|Zeq|xω ⇔ C=1/19.1x2xπx10e6=833 pF
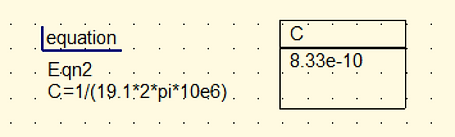.png)
Figure 11 : Equation condensateur THD
Comme précédemment, nous créons un circuit équivalent, ici il suffit de mettre un générateur avec le condensateur. Nous calculons également l’impédance Z2 du coefficient de réflexion S[2,2].
.png)
Figure 12 : Calcul condensateur équivalent THD
On trace ensuite Z2 sur le même graphe que le module et on veut que la droite passe par le point choisi précédemment (10 MHz, 19.1).
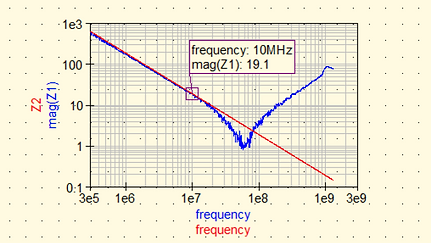.png)
Figure 13 : Tracé condensateur équivalent THD
Ici, on observe que notre droite en rouge passe bien par le point marqué avec le marqueur et épouse bien la forme de la partie capacitive de la courbe. On en conclut donc que notre calcul est le bon.
Ensuite on passe sur la partie résistive, on trouve ça valeur graphiquement, sur la courbe du module, on place le curseur sur la “pointe” de la courbe et la valeur du module est la valeur de la résistance car l’impédance d’une résistance est la résistance elle même donc le module de l’impédance est la résistance également.
.png)
Figure 14 : Tracé résistance équivalent THD
Ici, on a donc une résistance de 0.8 Ohm.
Dans un troisième temps, nous avons calculé la valeur de la bobine parasite. Pour cela, nous avons placé un curseur sur la courbe du module à l’endroit où l’on peut avoir la fréquence de résonance et nous avons relevé la valeur de la fréquence.
.png)
Figure 15 : Fréquence de résonance condensateur THD
On connaît l’équation pour trouver la fréquence de résonance ainsi que sa valeur.
f0=1/2xπx√(LC)=58.4 MHz
⇔ L=1/(2xπx58.4e6)²xC
⇔ L=9.04 nH
.png)
Figure 16 : Equation inductance parasite condensateur THD
Comme précédemment, nous créons un circuit équivalent, ici il suffit de mettre un générateur avec la bobine. Nous calculons également l’impédance Z3 du coefficient de réflexion S[3,3].
.png)
Figure 17: Calcul inductance parasite condensateur THD
On trace ensuite Z3 sur le même graphe que le module et Z2, et on veut que la droite passe par la partie inductive du module.
.png)
Ici, on observe que notre droite en vert épouse bien la forme de la partie inductive de la courbe. On en conclut donc que notre calcul est le bon.
Figure 18 : Tracé inductance parasite condensateur THD
Maintenant, nous avons toutes les valeurs de nos composants, nous reprenons notre schéma équivalent et remplaçons les valeurs des composants par celle trouvée précédemment. On calcule Z4 avec la fonction rtoz et le coefficient de réflexion de S[4,4].
On calcule également = 2f, et Zeq notre impédance équivalente de tout le circuit.
.png)
Figure 19 : Schéma équivalent final condensateur THD
Pour finir on trace toutes les courbes pour voir si elle se superpose bien. On trace donc mag(Z1), mag(Zeq) et mag(Z4). et on obtient le graphe suivant.
.png)
Figure 20 : Tracé schéma équivalent condensateur THD
Toutes nos courbes se confondent, ce qui prouve que toutes nos valeurs sont les bonnes. On peut donc en conclure que l’on a réussi à partir d’un relevé de valeur sur un VNA à retrouver le schéma équivalent d’un composant et les valeurs de ses composants parasites.
La résistance traversante (THD)
Nous avons fait de même pour la résistance :
.png)
Figure 21 : Schéma équivalent résistance
Nous récupérons les valeurs du VNA, et faisons le circuit.
.png)
Figure 22 : Coefficient de réflexion résistance
On trace uniquement le module de Z1 car comme vu précédemment, la courbe de phase est là en information nous ne l’utilisons pas.
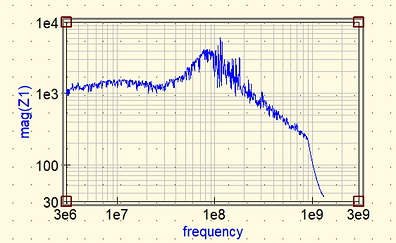.png)
Figure 23 : Comportement de l’impédance en fonction de la fréquence
Cette fois, pour avoir la valeur de la résistance, nous prenons notre curseur sur la partie plate de notre module.
.png)
Figure 24 : Mesure effet résistif résistance
Nous obtenons donc une valeur de 1k Ohm, en regardant ce qu’il y a de marqué sur la résistance, on compare les deux valeurs. La résistance est marquée 1k donc 1k Ohm. Donc nous avons la bonne valeur de R.
On s’occupe maintenant du condensateur parasite qui est en parallèle.
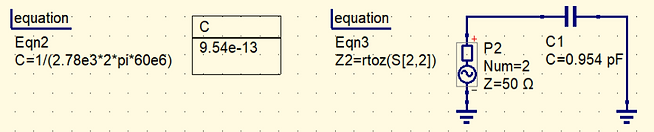.png)
Figure 25 : Calcul effet capacitif résistance
On a un condensateur de 0.954 pF. Maintenant on trace sur le premier graphe Z2.
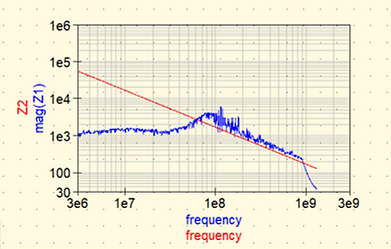.png)
Figure 26 : Mesure effet inductif résistance
On fait de même pour la bobine en série.
.png)
Figure 27 : Calcul effet inductif résistance
.png)
Figure 28 : Tracé effet capacitif et inductif résistance
On passe maintenant au schéma équivalent. On met les bonnes valeurs, on calcule Zeq et on simule les trois courbes.
Zeq= R+jωL
1+jRCω+(jω)²xLC
.png)
Figure 29 : Equation du schéma équivalent de la résistance
.png)
Figure 30 : Tracé du calcul du schéma équivalent de la résistance
Toutes nos courbes se confondent, ce qui prouve que toutes nos valeurs sont les bonnes.
On peut donc en conclure que l’on a réussi à partir d’un relevé de valeur sur un VNA à retrouver le schéma équivalent d’un composant et les valeurs de ses composants parasites.
Méthode 2 (méthode “tuning”) :
• Dans un premier temps nous importons les mesures du condensateur CMS et on convertit par équation le coefficient de réflection en impédance.
• On trace ensuite le graphique de l’impédance de ce schéma.
• Ce qui nous permet de dessiner le schéma équivalent du condensateur en approximant les valeurs de chacun des composants. on convertit par équation le coefficient de réflection en impédance.
• Pour tracer le graphique de l'impédance de ces deux schéma électrique (La mesure et le schéma équivalent).
• On utilise ensuite l'outil "Tune" qui effectue des simulations en boucle. Cet outil est très utile pour faire varier la valeur des composants.
• La courbe du graphique correspondant au schéma équivalent varie en fonction de la valeurs des composants et donc de l’outil tune.
• Nous faisons donc varier la valeur de chacun d’entre eux pour superposer les deux courbes.
• Une fois la courbe superposée nous avons donc une approximation de la valeurs des composants du schéma équivalent comme souhaité.
Approximation du schéma équivalent de la bobine par méthode “tuning”

Figure 31 : Calcul Schéma équivalent de la bobine
Approximation du schéma équivalent du condensateur CMS par méthode “tuning”
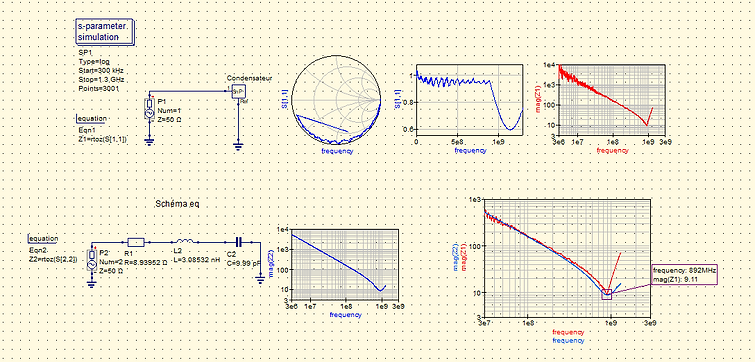
Figure 32 : Calcul Schéma équivalent condensateur CMS
Approximation du schéma équivalent du quartz par méthode “tuning”
.png)
Figure 33 : Coefficient de réflexion quartz
.png)
Figure 34 : tracé théorique quartz
.png)
Figure 35 : Tracé mesure du quartz
.png)
Figure 36 : Schéma équivalent quartz
.png)
Figure 37 : Tracé schéma équivalent quartz
D- Conclusion et problèmes rencontrés
Conclusion
Avec ce travail, nous avons pu approfondir nos compétences en électronique mais aussi sur le logiciel QucsStudio. Nous avons pu voir plus en détail les circuits équivalents des composants passifs réels, ainsi que l’importance de la place et de la valeur des composants dans un circuit.
Problèmes rencontrés
Sur nos prises de mesure, nous avons beaucoup de bruit malgré plusieurs prises pour limiter un maximum et avoir les meilleures mesures possible.
Ce problème après discussion avec nos professeurs vient probablement de l’appareil utilisé qui à tendance à avoir beaucoup de bruit.
Ce problème ne nous a pas dérangé pour la suite du TP mais nous avions des courbes très bruitées. Ce qui peut, sur un autre exercice avec beaucoup plus de mesure a faire sur les courbes, être dérangeant.
Un deuxième problème rencontré était sur le nombre de mesures notamment sur le quartz, nous nous sommes rendu compte trop tard que nous n’avions pas assez de mesures dans les fréquences les plus hautes.
Ce qui fait que notre courbe n'était pas la plus optimale.
La prochaine fois, il faudra que l’on fasse plus attention au nombre de points de mesure que l’on fait pour avoir de bonne courbes et donc plus de facilité pour la détermination des valeurs des composants.