

TP propagation dans un câble coaxiale
Un travaux pratique sur l'identification et la réalisation d'une datasheet d'un composant inconnue.
La caractérisation de composants a pour objectif de déterminer les caractéristiques électriques de fonctionnement d’un composant.
Table des matières
A- Mesure de l’atténuation dans un câble coaxial
La première partie de ce TP consiste en la mesure de l'atténuation du câble coaxial.
Les pertes dans le câble dépendent de la fréquence.
En régime continu ou aux très basses fréquences, la résistance linéique r (en m-1) s’écrit simplement r = p/S où S est la section réelle du conducteur.
Aux hautes fréquences, il faut tenir compte de l’effet de peau et la résistance linéique r augmente avec la fréquence.
La densité de courant n’est plus homogène dans le conducteur, le courant circule uniquement à la périphérie, la section utile au passage du courant devient inférieure à S.
1. Mesures préliminaires
On connecte le générateur de fonction à l'oscilloscope via un câble d'impédance caractéristique Zc=50 et de longueur environ 50 cm comme indiqué sur la figure 1.

Figure 36 : Branchement à effectuer pour les mesures préliminaires
On règle sur le générateur de fonction un signal sinusoïdal d'amplitude 6 Vcc et de fréquence f=1 kHz. On visualise le signale suivant (Figure 37), on mesure bien un signal sinusoïdal d’amplitude 6 Vcc et de fréquence 1kHz.
.png)
Figure 37
On place maintenant le bouchon 50 Ohms sur un Té BNC à l'entrée de la voie 1 de l'oscilloscope.
On visualise le signal suivant :
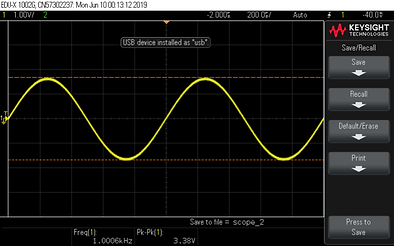.png)
Figure 38
Avec le théorème de Thévenin, on calcul notre nouvelle tension d’entrée ainsi que la résistance équivalente.
Le bouchon de 50 Ohm permet donc de diminuer la tension d’entrée de moitié, on a un gain de 0.5.


_edited_edited.png)
Figure 39 : Schéma équivalent par Thevenin
2. Mesures de l'atténuation aux très basses fréquences
On connecte le générateur de fonction à l'oscilloscope via un câble d'impédance caractéristique ZC=50 et de longueur environ 50 cm.
Le tout connecter par l'intermédiaire d'un Té BNC à l'entrée du câble de 100m de longueur à la voie 1 de l'oscilloscope.
On utilise la fonction “save” de l'oscilloscope pour pouvoir simuler trois entrées car il n’en possède que deux.
On connecte donc ensuite sur la voie 1 le point milieu du câble et sur la voie 2 on connecte l'extrémité du câble et le bouchon 50 avec un Té BNC (Cf figure 40).
_edited.png)
Figure 40 : Branchement à effectuer pour la mesure de l’atténuation à très basse fréquence
On règle le générateur de fonction pour obtenir 6Vcc sur l’écran de l’oscilloscope en entrée de ligne. On mesure :
.png)
Courbe orange (R1) = entrée câble coax
Courbe verte Voie 2 = milieux câble coax
Courbe jaune Voie 1 = sortie du câble coax
Figure 41
3. Mesures de l'atténuation en fonction de la fréquence
On souhaite analyser l'atténuation du câble coaxial en fonction de la fréquence. On conserve les branchements réalisés pour les manipulations précédentes mais on fait varier la fréquence du signal sinusoïdal de 100Hz à 20MHz.
On mesure V1 (entrée du câble) et V3 (sortie du câble) pour les différentes fréquences du tableau 1.

Tableau 1 : Mesure atténuation fréquentielle du câble
On utilise la fonction générateur de l’oscilloscope (“analyse”) pour représenter l'atténuation du câble (en dB/100m) pour chaque fréquence. Cette fonction permet de mesurer sur une grande plage de fréquence avec une plus grande précision. Elle nous permet également de tracer la courbe automatiquement.
On obtient la mesure suivante :
.png)
Figure 42 : Mesure atténuation fréquentielle du câble
B- Propagation en régime impulsionnel
1. Détermination des constantes linéiques d'un câble coaxial
On effectue le branchement suivant en laissant la fin du câble ouverte pour nous permettre d’avoir une impédance infinie. On veut avoir trois courbes sur l’oscilloscope, donc on utilise la fonction “ref” pour sauvegarder la courbe du milieu de notre câble.
_edited_edited.png)
Figure 43
On met au générateur de fonction un pulse d’amplitude 4V, de durée 400ns et de fréquence 100kHz. Si on le branche directement à l’oscilloscope, nous observerons la courbe suivante.
_edited.png)
Figure 44
.png)
Figure 45

En reconnectant l’entrée de la ligne sur l’entrée du générateur, on obtient les courbes précédentes. On peut alors mesurer la durée de propagation de l’onde d’un bout à l’autre de l’antenne.
Comme vu en cours, la vitesse de propagation dans un câble est de 2.108 donc on retrouve le même résultat.
On charge l'extrémité du câble par une résistance ajustable de 0 à 100 Ohms et on règle sa valeur jusqu'à atteindre la disparition des impulsions réfléchies (Figure 46).
.png)
Figure 46
On mesure ensuite la valeur de la résistance variable avec l'ohmètre.
On mesure une résistance de 56.8 Ohms.
On peut donc en déduire la valeur de l'impédance car à 56.8 Ohm nous avons plus d'impulsions réfléchis, ce qui signifie que l’on est à adaptation d’impédance et que tout l’énergie envoyée est utilisée.
Donc l’impédance caractéristique (Zc) est de 56.8 Ohm. Or sur la datasheet du câble on nous informe d’une impédance de 50 Ohm. Nous avons donc une erreure de 6.8 Ohm qui peut venir des différents té utilisés.
Maintenant que nous avons Zc (on prendra Zc à 50 Ohm pour limiter le cumul d’erreurs), nous pouvons calculer les constantes linéiques de C et de L. Pour cela on résout un système car on sait que :

On obtient donc le système à deux équations à deux inconnues.
_edited.png)
Dans les datasheets, le fournisseur nous donne la constante linéique de C = 100 pF/m ainsi que l'impédance caractéristique de 50 Ohm. On calcule donc L avec ces valeurs et on retrouve le même résultat.
2. Transmission d'impulsions dans un câble coaxial : réflexion et adaptation
Nous venons de caractériser les paramètres physiques du câble coaxial. Nous allons à présent étudier la transmission d'impulsions en fonction de différents types d'impédance de charge. On utilise les mêmes conditions d'excitation du câble coaxial que précédemment.
L'extrémité du câble étant ouverte (Figure 43), On relève :
.png)
Courbe jaune Voie 1 = entrée câble coax
Courbe orange (R1) = Milieux cable coax
Courbe verte Voie 2 = sortie câble coax
Figure 47 : Mesure circuit ouvert
L'extrémité du câble étant court-circuitée, on retire le bouchon 50 sur le Té BNC en voie 1. On relève :
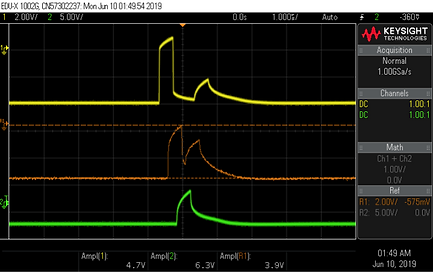.png)
Courbe jaune Voie 1 = entrée câble coax
Courbe orange (R1) = Milieux cable coax
Courbe verte Voie 2 = sortie câble coax
Figure 48 : Mesure circuit fermé
En entrée, nous avons une tension d’amplitude 4.7V qui diminue un peu pour passer à 3.9V en milieu de câble.
On remarque qu’il y a une augmentation de l’amplitude sur la fin du câble par rapport au début du câble, nous passons donc de 4.7V à 6.3V.
Cette augmentation peut être dû au coefficient de réflexion qui nous renvoie une tension.
Cette tension peut alors se multiplier à notre tension d’entrée ce qui nous donne une augmentation d’amplitude et une modification du signal.
C- Conclusion et problèmes rencontrés
Conclusion
Avec ce travail, nous avons pu mettre en pratique tout ce que nous avions vu en cours théorique, notamment tous les principes d’un câble coaxial et des coefficients de réflexions. Nous avons également pu approfondir nos compétences en électronique.
Problèmes rencontrés
Sur ce TP, nous avons été principalement embêtés par le câble de 100m qui était endommagé.
Le problème a été découvert lors des visualisations sur l’oscilloscope, nous n’avions pas les bons signaux et surtout, lorsque nous bougions le câble les courbes changeaient.
Le problème pouvait donc venir des Tés ou du câble, nous sommes donc partie de la base problème donc ici du connecteur à l’oscilloscope et ensuite nous avons remonté le circuit pour voir d’où vient la cause du problème.
Une fois déterminé, nous pouvons essayer de le résoudre. Ici il faudrait changer de câble, le nombre étant limité, nous ne pouvions pas le faire. Nous aurions aussi pu le réparer mais par manque de temps et par complexité des connecteurs nous ne l’avons pas fait.
Le deuxième problème, venait de la résistance variable qui n’avait aucun effet sur les courbes et sur le circuit.
En regardant de plus près il y avait simplement un écrou de dévisser ce qui entraîne un faux contacte.
Nous l’avons donc simplement resserré.